Question

Determine the speed of the Earth in its motion around the Sun using Newton's Law of Universal Gravitation and centripetal force. Look up the values of the Earth's mass, the Sun's mass, and the average distance of Earth from the Sun; other than G, nothing else is needed

Answer 1

In order to determine the speed of the Earth, proceed as follow:

Consider that the centripetal force must be equal to the gravitational force between the Earth and the Sun (because guarantees the stability of the system):

`F_g=F_c`

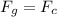
Fg is the gravitational force and Fc the centripetal force. The expressions for each of these forces are:

`\begin{gathered} F_g=\text{G}\frac{\text{mM}}{r^2} \\ F_c=ma_c=m(v^2)/(r) \end{gathered}`

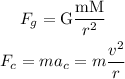
where,

G: Cavendish's constant = 6.67*10^-11 Nm^2/kg^2

m: Earth's mass = 5.97*10^24 kg

M: Sun's mass = 1.99*10^30kg

v: speed of Earth around the Sun = ?

r: distance between the center of mass of Earth and Sun = 1.49*10^8km = 1.49*10^11 m

Equal the expressions for Fg and Fc, solve for v, replace the previous values of the parameters and simplify:

Hence, the speed of the Earth around the Sun is approximately 29846.7m/s