Question

Select the procedure that can be used to show the converse of the Pythagorean theorem using side lengths chosen from 6 feet, 8 feet, 10 feet, and 11 feet.

Answer 1

Answer: Choice A

========================================================

Step-by-step explanation:

The left side
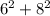`6^2+8^2` simplifies to
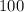`100` since
`6^2+8^2 = 36+64 = 100`

The right side is also 100 because
`10^2 = 100`

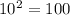
So
`6^2+8^2 = 10^2` is a true equation because both sides are the same number.

Therefore, a triangle with sides 6,8,10 is a right triangle. The hypotenuse 10 is the longest side opposite the 90 degree angle. In other words, the 90 degree angle is between the sides 6 ft and 8 ft.

So this is why choice A is the final answer.

-----------

Choice B is false because the inequality
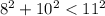`8^2+10^2 < 11^2` becomes
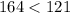`164 < 121` which is also false. Even if that inequality was true, we can't use it to form a right triangle. We need both sides to be equal.

Choice C is false because we need to have both sides equal to the same number. We need to have
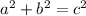`a^2+b^2 = c^2` to be true if we want a right triangle with sides a,b,c.

Choice D is false because of the phrasing "Draw any two of the sides with a right angle between them". The 90 degree angle must go between the 6 and the 8, and nowhere else.