Question

Lines PQ and Rs are parallel. Find y. P(2, -5); Q(5, 6); R(3, -1); S(6, y)y = ?

Answer 1

To answer this question it is necessary to find the equation of the given lines

Find the equation for PQ. To do it, find the slope of the equation:

`m=(6-(-5))/(5-2)=(11)/(3)`

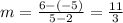
Now, use the point slope formula to find the equation of the line:

`\begin{gathered} y-6=(11)/(3)(x-5) \\ y=(11)/(3)x-(55)/(3)+6 \\ y=(11)/(3)x-(37)/(3) \end{gathered}`

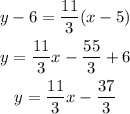
Parallel lines have the same slope, it means PQ and RS have the same slope, then RS has a slope of 11/3

Use the point slope formula to find the equation of the line RS:

`\begin{gathered} y-(-1)=(11)/(3)(x-3) \\ y+1=(11)/(3)x-11 \\ y=(11)/(3)x-12 \end{gathered}`

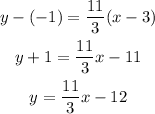
Now, use this equation to find y when x is 6 (which corresponds to point S):

`\begin{gathered} y=(11)/(3)x-12 \\ y=(11)/(3)(6)-12 \\ y=22-12 \\ y=10 \end{gathered}`

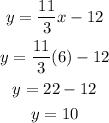
y has a value of 10.