Question

Solve 5x^2 - 7x + 2 = 0 by completing the square.

What is the constant added on to form the perfect square trinomial?

a. 49/4
b. 49/25
c. 49/100

Answer 1

I guessed this answer was 49/100 in my lesson because my lesson gave some info to help. The answer I guessed was correct so there you go to answers to verify this is correct :)

Explanation:

Answer 2

Answer: The correct option is (c)
`(49)/(100).`

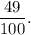
Step-by-step explanation: We are given to solve the following quadratic equation by the method of completing the square:

`5x^2-7x+2=0~~~~~~~~~~~~~~~~~~~(i)`

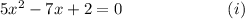
Also, we are to find the constant added on both sides to form the perfect square trinomial.

We have from equation (i) that

`5x^2-7x+2=0\\\\\Rightarrow x^2-(7)/(5)x+(2)/(5)=0\\\\\\\Rightarrow x^2-2* x* (7)/(10)+\left((7)/(10)\right)^2+(2)/(5)=\left((7)/(10)\right)^2\\\\\\\Rightarrow \left(x-(7)/(10)\right)^2=(49)/(100)-(2)/(5)\\\\\\\Rightarrow  \left(x-(7)/(10)\right)^2=(49-40)/(100)\\\\\\\Rightarrow  \left(x-(7)/(10)\right)^2=(9)/(100)\\\\\\\Rightarrow x-(7)/(10)=\pm(3)/(10)\\\\\\\Rightarrow x=\pm(3)/(10)+(7)/(10).`

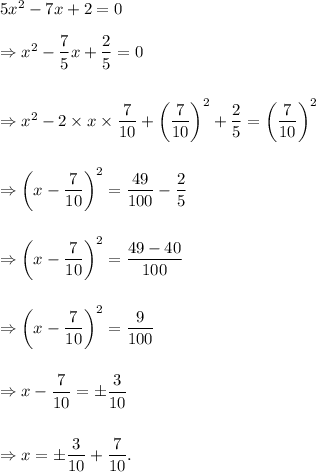
So,

`x=(3)/(10)+(7)/(10),~~~~~~~~x=-(3)/(10)+(7)/(10)\\\\\\\Rightarrow x=(10)/(10),~~~~~~~~\Rightarrow x=(-3+7)/(10)\\\\\\\Rightarrow x=1,~-(2)/(5).`

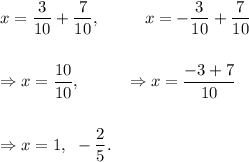
Thus, the required solution is
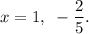`x=1,~-(2)/(5).` and the value of the constant added is
`(49)/(100).`

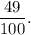
Option (c) is correct.