Since about 95% of a normal distribution falls within two standard deviations of the mean
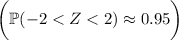
, it follows that 5% lie outside this range, with 2.5% lying to either side of it.This means
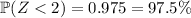
, with the remaining 2.5% lying above
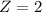
.
This means for a score to belong in the top 2.5%, it's corresponding z-score must be higher than 2.
Fred scores 13.1 on the test. The corresponding z-score is
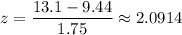
which is barely higher than 2, but high enough to earn that certificate.