Question

Please no dumb answers. I really do need help. And correct answers.

f(x)=-32(2)^(x-3)+3 find the y-intercept?

What is the exponential form of the logarithmic equation?
4=log0.80.4096

What is the value of the logarithm?
log(750)

Round the answer to the nearest thousandth.
Solve the logarithmic equation.
y=log40.25

Answer 1

y intercept is where x=0

so
-32(2^-3)+3
-32(1/(2^3))+3
-32(1/8)+3
-4+3
-1
yint is (0,-1)



log thing

assuming you meant
`4=log_(0.80)(0.4096)` (because I can't read what that is supposed to be )
remember that
`a=log_b(c)` tarnalsates to
`b^a=c` so den

`4=log_(0.80)(0.4096)` means
`4^(0.4096)=0.80`





log(750)
when no base is mentinoed, assume base of 10
I would just use my calculator tho

`log_(10)(750)=?`
translate

`10^?=750`
I do know that 2<?<3 tho, that's all I know
if we did use a calculator then the aproxamate value is 2.875






y=log40.25
10^y=40.25
know taht 1<y<2
dunno what else
sorry
if we use calcualtor it's about 1.604

Answer 2

1. y-intercept is -1.

2. Exponential form is
`0.80^(4)=0.4096`.

3. 2.875

4. y = 0.873

Explanation:

1. We have the function
`f(x) = -32 * 2^(x-3) +3`.

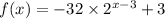Now as we know that y-intercept is the point where the line cuts y-axis i.e. x=0.

So, x=0 in the
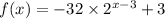`f(x) = -32 * 2^(x-3) +3` gives,

`f(x) = -32 * 2^(0-3) +3`

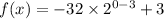
i.e.
`f(x) = (-32)/(2^(3))+3`

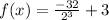
i.e.
`f(x) = (-32)/(8)+3`

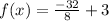
i.e.
`f(x) = -4+3`

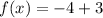
i.e.
`f(x) = -1`

So, the y-intercept of this function is -1.

2. We have,
`4=log_0.80(0.4096)`

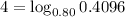
As,
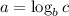`a=\log_(b)c` implies
`b^(a)=c`.

Therefore,
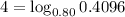`4=\log_(0.80)0.4096` implies
`0.80^(4)=0.4096`.

Hence, the exponential form is
`0.80^(4)=0.4096`.

3. We have to find the value of log(750).

As no base is given, we assume the base to be 10.

So,
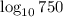`\log_(10)750` = 2.875.

4. We have,
`y=log_40(25)`

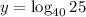
Again using, As,
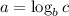`a=\log_(b)c` implies
`b^(a)=c`.

We have, As,
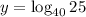`y=\log_(40)25` implies
`40^(y)=25`

i.e.
`y * \log40 = \log25`

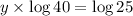
i.e. y = 0.87258905175

Rounding to nearest thousand gives y = 0.873.