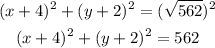Question

Write the equation of the circle centered at (−4,−2) that passes through (−15,19)

Answer 1

In this problem, we are going to find the formula for a circle from the center and a point on the circle. Let's begin by reviewing the standard form of a circle:

`(x-h)^2+(y-k)^2=r^2`

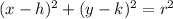
The values of h and k give us the center of the circle, (h,k). The value r is the radius. We can begin by substituting the values of h and k into our formula.

Since the center is at (-4, -2), we have:

`\begin{gathered} (x-(-4))^2+(y-(-2))^2=r^2 \\ (x+4)^2+(y+2)^2=r^2 \end{gathered}`

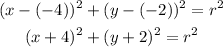
Next, we can use the center and the given point on the circle to find the radius.

Recall that the radius is the distance from the center of a circle to a point on that circle. So, we can use the distance formula:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

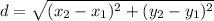
Let

`(x_1,y_1)=(-4,-2)`

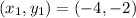
and let

`(x_2,y_2)=(-15,19)`

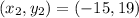
Now we can substitute those values into the distance formula and simplify.

`\begin{gathered} r=√((-15-(-4))^2+(19-(-2))^2) \\ r=√((-11)^2+(21)^2) \\ r=√(562) \end{gathered}`

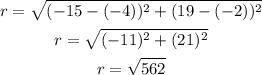
Adding that to our equation, we have:

`\begin{gathered} (x+4)^2+(y+2)^2=(√(562))^2 \\ (x+4)^2+(y+2)^2=562 \end{gathered}`