Hello there. To solve this question, we'll have to remember some properties about triangles.
Given the triangle:
Notice in this case we have two consecutive angles and a side between them. This is a case of ASA (angle-side-angle).
With respect to the side with measure x, we have two consecutive angles then the side, hence AAS.
To find x, we'll have to apply the law of sines:
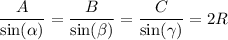
In this case, the angle opposite to x measures 73º and the angle opposite to 4 measures 85º, hence:
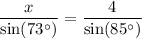
Multiply both sides by a factor of sin(73º)
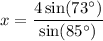
Using a calculator, we get the following approximation (rounding to the nearest tenth):
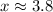
This is the measure of x we're looking for.