Question

(I don't know if there are tutors here right now at this time but it's worth a try.) Please help me I really really don't understand this, it's going to take me a while to understand this. X(

Answer 1

`\begin{gathered} 3(b+5)=4(2b-5) \\ 3b+15=8b-20 \\ 15+20=8b-3b \\ 5b=35 \\ b=(35)/(5) \\ b=7 \end{gathered}`
`3(b+5)=4(2b-5)`

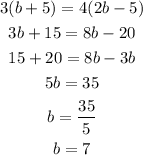
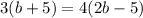
by the distributive law x(y+z)=zy+xz, we have

`\begin{gathered} 3b+3(5)=4(2b)-4(5) \\ 3b+15=8b-20 \end{gathered}`

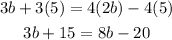
Then we use the properties of inequalities, we can switch both sides, and if we add or multiply something on both sides the equality remains

`\begin{gathered} 3b+15=8b-20 \\ \end{gathered}`

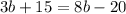
we want the variables and the numbers without variables to be in different side, so, first we add 20 to both sides, note that the -20 will be cancelled

`\begin{gathered} 3b+15+20\text{ = 8b-20+20} \\ 3b+15+20=8b \end{gathered}`

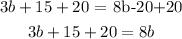
we want to left all the numbers with variable on the right side so we substract 3b (add -3b) to both sides. Same as before, the 3b will be cancellated (we can change the order in the sum)

`\begin{gathered} -3b+3b+15+20=-3b+8b \\ 15+20=8b-3b \end{gathered}`

of course, you're welcome

I was asking if you have understood my explanation so far

tell me

it doesn't matter the order, in fact, when you get used to the method you can work with both at the same time

any other question?

yes, you could substrac 3b first

For example

`\begin{gathered} 2+3x=6-x \\ 2+3x+x=6-x+x \\ 2+3x+x=6 \\ -2+2+3x+x=-2+6 \\ 3x+x=6-2 \\ 4x=4 \\ \end{gathered}`

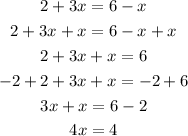
sadly I will need to leave since my shift is over, but if you ask another question one of my partners will help you

Have a nice evening!!!!

then we add like terms and switch both sides

`5b=35`

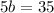
And then we multiply by 1/5 both sides

`\begin{gathered} 5(1)/(5)b=(35)/(5) \\ b=(35)/(5) \\ b=7 \end{gathered}`