Question

Find all solutions in[0, 2pi): 2sin(x) – sin (2x) = 0

Answer 1

Based on the answer choices, replace the pair of given values and verify the equation, as follow:

For x = π/4, π/6

`2\sin ((\pi)/(4))-\sin ((2\pi)/(4))=2\frac{\sqrt[]{2}}{2}-1\\e0`

the previous result means that the given values of x are not solution. The answer must be equal to zero.

Next, for x = 0, π

`\begin{gathered} 2\sin (\pi)-\sin (2\pi)=0-0=0 \\ 2\sin (0)-\sin (0)=0-0=0 \end{gathered}`

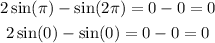
For both values of x the question is verified.

The rest of the options include π/4 and π/3 as argument, you have already shown that these values of x are not solution.

Hence, the solutions for the given equation are x = 0 and π