Let
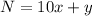
, so that

is the digits in the tens place and

is the digit in the ones place. (Clearly
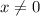
.)
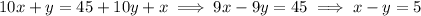
There are five possible two digits integers that satisfy this relation:
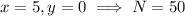

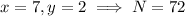

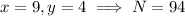
But the first, third, and fifth candidates are even, so they are not prime. The remaining are prime, however, so
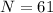
or
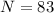
.