The height of the ball at any time t is given by
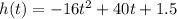
This is a quadratic equation, which attains its maximum value at time:
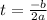
In the given equation, a = -16 and b = 40. substitute these values in the formula:
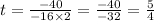
Therefore, the ball attains its maximum height at t=5/4 seconds which is given below:
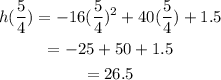
Thus, the maximum height attained by the ball is 26.5 feet.