Question

Let f: R - {2} => RX => f (x) = (3x + 4) / (x-2)Is F a bijection?

Answer 1

A function is called bijective if it is one-to-one and onto.

To check one to one, let x1 = x2 , where x1, x2 belongs to R.

so, we can say that:

`3x_1+4=3x_2+4`

and

`x_1-2=x_2-2`

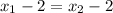
Given the condition that x1 and x2 are not equal to 2. So, the above equation implies that

`(3x_1+4)/(x_1-2)=(3x_2+4)/(x_2-2)\Rightarrow f(x_1)=f(x_2)`

So, it is a one-to-one function.

For onto function, let y= (3x + 4) / (x-2). Now, interchange x and y, and solve the equation fo y:

`\begin{gathered} x=(3y+4)/(y-2) \\ \Rightarrow xy-2x=3y+4 \\ \Rightarrow xy-3y=2x+4 \\ \Rightarrow y(x-3)=2x+4 \\ \Rightarrow y=(2x+4)/(x-3) \end{gathered}`

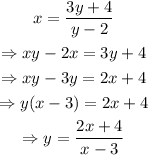
Here, the domain of the inverse of the function is R - {3}. But the function is R - {2} => R. So, it is not onto.

thus, the given function is not a bijection.