Question

Is binomial Theorem JUST Pascal's triangle? Or is there another equation...?

Answer 1

Pascal's triangle is a visual representation of the coefficients involved in a binomial expansion. The
`n`th row of the triangle gives the coefficients of the terms in the expansion of
`(a+b)^(n-1)`.

The triangle itself looks like


`\begin{matrix}1\\1&1\\1&2&1\\1&3&3&1\end{matrix}`

and so on, while the expansions for
`n=1,2,3,4` are


`(a+b)^(1-1)=(a+b)^0=1`

`(a+b)^(2-1)=(a+b)^1=1a+1b`

`(a+b)^(3-1)=(a+b)^2=1a^2+2ab+1b^2`

`(a+b)^(4-1)=(a+b)^3=1a^3+3a^2b+3ab^2+1b^3`

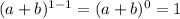
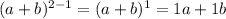
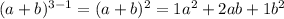
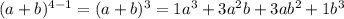
and so on.

The binomial theorem says that


`(a+b)^(n-1)=\displaystyle\sum_(k=0)^(n-1)\binom{n-1}ka^(n-1-k)b^k`

`(a+b)^(n-1)=\dbinom{n-1}0a^(n-1)b^0+\dbinom{n-1}1a^(n-2)b^1+\cdots+\dbinom{n-1}{n-2}a^1b^(n-2)+\dbinom{n-1}{n-1}a^0b^(n-1)`

`(a+b)^(n-1)=\dbinom{n-1}0a^(n-1)+\dbinom{n-1}1a^(n-2)b+\cdots+\dbinom{n-1}{n-2}ab^(n-2)+\dbinom{n-1}{n-1}b^(n-1)`

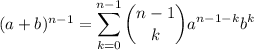
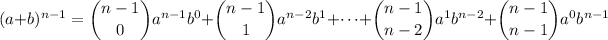
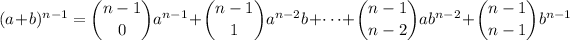
The numbers in the
`n`th row of the triangle are just
`\dbinom{n-1}k`, with
`k=0,1,\ldots,n-2,n-1`.

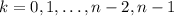
So no, the binomial theorem and Pascal's triangle are not the same thing. Pascal's triangle is a way of organizing the pattern exhibited by the result of the binomial theorem.