Question

a company earns a weekly profit of p dollars by selling x items, according to the equation p(x)=-0.5x^2+40x-300 how many items does the company have to sell each week to maximize its profit

Answer 1

legit way is vertex form

easy way is this
x value of vertex in form
f(x)=ax^2+bx+c is -b/2a
the y value is f(x value of vertex)

so

p(x)=-0.5x^2+40x-300
x value of vertex is -40/(2*-0.5)=-40/-1=40


max profit selling 40 per week
profit would be 500

Answer 2

The company have to sell 40 items each week to maximize its profit.

Explanation:

The given profit function is

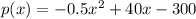`p(x)=-0.5x^2+40x-300` .... (1)

where, p is weekly profit in dollars and x is number of sold items.

In the given function leading coefficient is negative, it means it is a downward parabola and vertex of a down word parabola is point of maxima.

If a parabola is defined as

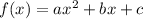`f(x)=ax^2+bx+c` .... (2)

then the function is maximum at
`x=-(b)/(2a)`.

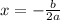From (1) and (2) we get

`a=-0.5, b=40, c=300`

`x=-(b)/(2a)=-(40)/(2(-0.5))=40`

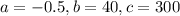
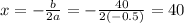
The given function is maximum at x=40.

Therefore the company have to sell 40 items each week to maximize its profit.