Answer:
The car is 6.5788 years old.
Explanation:
The key to solve the problem is in the following sentence: "The value of a car is half what it originally cost". Keep in mind that
 is the current value and
is the current value and
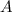 is the original cost. It means that
is the original cost. It means that
 is half of
is half of
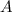 :
:
 .
.
It is assumed that the rate of depreciation is annually and its value is
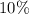 . Remember that
. Remember that
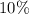 equals
equals
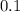 , so
, so
 .
.
For finding the value of
 , you must replace the values of
, you must replace the values of
 and
and
 in the depreciation formula:
in the depreciation formula:
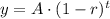
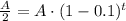
After cancelling the variable
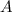 the equation would be:
the equation would be:
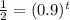
For finding the value of
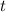 you must apply natural algorithm in both sides:
you must apply natural algorithm in both sides:
![ln\bigg( (1)/(2)\bigg) =ln[(0.9)^t]](https://img.qammunity.org/2018/formulas/mathematics/high-school/te8nkjcyft0bnwbwdrxfm2ckit79oa9vjx.png)
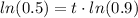
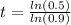

The previous value can be split in two parts:
 . The first part refers to years and the second part can be converted to months by multiplying the total months in a year (
. The first part refers to years and the second part can be converted to months by multiplying the total months in a year (
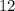 ) by
) by
 .
.
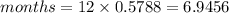
Thus, the car is 6.5788 years old (which is approximately 6 years and almost 7 months).