Question

A segment in the complex plane has a midpoint at –1 + i. If the segment has an endpoint at –5 – 7i, what is the other endpoint?

Answer 1

The midpoint formula is simply
ma = (a1 + a2)/2
mb =(b1 + b2)/2
The midpoint is -1 + i and the other endpoint is -5 - 7i
The other endpoint is
-1 = (-5 + a2)/2
a2 = 3
1 = (-7 + b2)/2
b2 = 9

3 + 9i

Answer 2

The other end point is: s+ti = 3+9i

Explanation:

Mid-Point(M) in the complex plane states that the midpoint of the line segment joining two complex numbers a+bi and s+ti is the average of the numbers at the endpoints.

It is given by:
`M = (a+s)/(2) +((b+t)/(2))i`

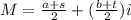
Given: The midpoint = -1 + i and the segment has an endpoint at -5 - 7i

Find the other endpoints.

Let a + bi = -5 -7i and let other endpoint s + ti (i represents imaginary )

Here, a = -5 and b = -7 to find s and t.

then;

`-1+i = (-5+s)/(2) + ( (-7+t)/(2))i` [Apply Mid-point formula]

On comparing both sides

we get;

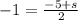`-1 = (-5+s)/(2)` and
`1 = (-7+t)/(2)`

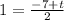
To solve for s:

`-1 = (-5+s)/(2)`

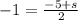
or

-2 = -5+s

Add 5 to both side we have;

-2+5 = -5+s+5

Simplify:

3 = s or

s =3

Now, to solve for t;

`1 = (-7+t)/(2)`

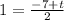
2 =-7+t

Add 7 to both sides we get;

2+7 = -7+t+7

Simplify:

9 = t

or

t =9

Therefore, the other end point (s+ti) is, 3+9i