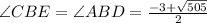Question

Find the measure of angle CBE.

Answer 1

so... what would that angle be? namely, ABD + ABC

CBE = ABD <--- vertical angles
thus
CBE = x + 56

and CBE + ABC = 180
or

`\bf (x+56)+(x^2+2x)=180\implies x^2+3x+56-180=0 \\\\ x^2+3x-124=0`

Answer 2

Answer:
`\angle CBE=(-3+√(505))/(2)`

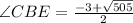
Explanation:

Given :

`\angle ABD=x+56\\\angle ABC=x^2+2x`

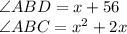
To find :
`\angle CBE`

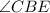
Solution:

As
`\angle ABD\,,\,\angle ABC` lie on a straight line ,

`\angle ABD+\angle ABC=180^(\circ)`

`x+56+x^2+2x=180\\x^2+3x+56-180=0\\x^2+3x-124=0`

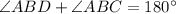
We will solve this equation using quadratic formula:

For equation
`ax^2+bx+c=0`, roots are given by
`x=(-b\pm √(b^2-4ac))/(2a)`

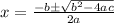
Solving equation:
`x^2+3x-124=0`

`x=(-3\pm √(9+496))/(2)=(-3\pm √(505))/(2)`

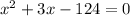
As value of angle can not be negative,
`x\\eq (-3- √(505))/(2)`

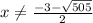
,so
`x= (-3+√(505))/(2)`

`\angle CBE= (-3+√(505))/(2)`

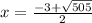
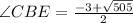
Also, as
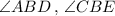`\angle ABD \,,\,\angle CBE` are vertically opposite angles,

`\angle CBE=\angle ABD=(-3+√(505))/(2)`