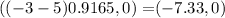Question

Write the equation below in standard form and then answer the following questions. If a value is a non-integer type your answer as a decimal rounded to the hundredths place. 4x^2+24x+25y^2+200y+336=0The center of the ellipse is (h,k). h= Answer and k= AnswerThe value for a is Answer . The value for b is Answer .The foci with the positive x value is the point ( Answer, Answer)The foci with the negative x value is the point ( Answer, Answer)

Answer 1

Given:

`4x^2+24x+25y^2+200y+336=0`

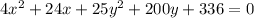
Aim:

We need to convert the given equation into the standard form of the ellipse equation.

Step-by-step explanation:

Consider the standard form of the ellipse equation.

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

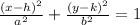
Consider the given equation.

`4x^2+24x+25y^2+200y+336=0`
`Use\text{ }336=36+400-100.`

`4x^2+24x+25y^2+200y+36+400-100=0`

`4x^2+24x+36+25y^2+200y+400-100=0`

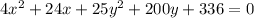
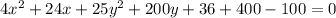
Take out the common terms.

`4(x^2+6x+9)+25(y^2+8y+16)-100=0`

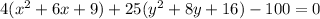
Add 100 on both sides of the equation.

`4(x^2+6x+9)+25(y^2+8y+16)-100+100=0+100`

`4(x^2+6x+9)+25(y^2+8y+16)=100`

`4(x^2+2*3x+3^2)+25(y^2+2*4y+4^2)=100`
`\text{Use (a+b)}^2=a^2+2ab+b^2.`

`4(x+3)^2+25(y+4)^2=100`

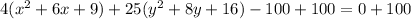
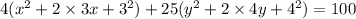
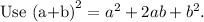
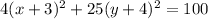
Divide both sides by 100.

`(4\mleft(x+3\mright)^2)/(100)+(25\mleft(y+4\mright)^2)/(100)=(100)/(100)`

`(\mleft(x+3\mright)^2)/(25)+(\mleft(y+4\mright)^2)/(4)=1`

`(\mleft(x+3\mright)^2)/(5^2)+(\mleft(y+4\mright)^2)/(2^2)=1`

`(\mleft(x-(-3)\mright)^2)/(5^2)+(\mleft(y-(-4)\mright)^2)/(2^2)=1`

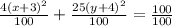
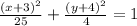
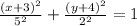
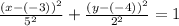
The standard form of the given equation is

`(\mleft(x-(-3)\mright)^2)/(5^2)+(\mleft(y-(-4)\mright)^2)/(2^2)=1`

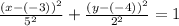
Compare with the general form of the ellipse equation.

We get h=-3, k=-4, a=5 and b=2.

The centre of the ellipse is h= -3 and k = -4.

The value of a is 5.

The value of b is 2.

We need to find the eccentricity of the ellipse.

`e=\sqrt[]{1-(b^2)/(a^2)}`

Substitute b=2 and a =5 in the formula.

`e=\sqrt[]{1-(2^2)/(5^2)}=\sqrt[]{1-(4)/(25)}=\sqrt[]{(25-4)/(25)}=\sqrt[]{(21)/(25)}=0.9165`
`e=0.9165`

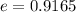
The foci of the ellipse are

`((h\pm a)e,0)`

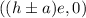
Substitute h =-3, a=5 and e =0.9165 in the formula.

`((-3\pm5)0.9165,0)`

The foci with a positive x value are the point

`((-3+5)0.9165,0)\text{ =}(1.83,0)`
`(1.83,0)`

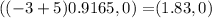
The foci with a negative x value are the point

`((-3-5)0.9165,0)\text{ =}(-7.33,0)`

`(-7.33,0)`