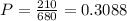Question

27. A race consists of 7 women and 10 men. What is the probability that the top three finishers were(a) all men (b) all women (c) 2 men and 1 woman (d) 1 man and 2 women

Answer 1

Given 7 women and 10 men;

a) the top 3 are all men:

`\begin{gathered} ways\text{ to choose 3 men out of 10 men is:} \\ 10C_3=(10!)/((10-3)!3!) \\ \Rightarrow(10!)/(7!3!)=(10*9*8*7!)/(7!*3*2*1) \\ \Rightarrow(10*9*8)/(3*2*1)=120 \\ \text{ways to choose 3 men from 17 people(10men +7women) is:} \\ 17C_3=(17!)/((17-3)!3!) \\ \Rightarrow(17!)/(14!*3!)=(17*16*15*14!)/(14!*3*2*1) \\ \Rightarrow(17*16*15)/(3*2*1)=680 \end{gathered}`

Therefore, the probability that the top 3 are all men is:

`P_{all\text{ men}}=(120)/(680)=0.1765`

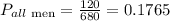
b) the top 3 are all women:

`\begin{gathered} \text{ways to choose 3 women from 7 women is:} \\ 7C_3=35 \\ \text{ways to choose 3 women from 17 people is:} \\ 17C_3=680 \end{gathered}`

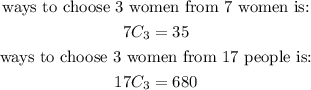
Therefore, the probability that the top 3 are all women is:

`P_{\text{all women}}=(35)/(680)=0.0515`

c) 2 men and 1 woman;

`\begin{gathered} ways\text{ to choose 2 men out of 10 men is:} \\ 10C_2=45 \\ \text{ways to choose 1 woman from 7 women is:} \\ 7C_1=7 \\ \text{Thus, ways to choose 2 men and 1 woman }=45*7=315 \end{gathered}`

Therefore, the probability that the top 3 finishers are 2 men and 1 woman is:

`P=(315)/(680)=0.4632`

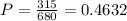
d) 1 man and 2 women;

`\begin{gathered} \text{ways to choose 1 man from 10 men is;} \\ 10C_1=10 \\ \text{ways to choose 2 women from 7 women is:} \\ 7C_2=21 \\ \text{Thus, ways to choose 1 man and 2 women is 10}*21=210 \end{gathered}`

Therefore, the probability that the top 3 finishers are 1 man and 2 women is:

`P=(210)/(680)=0.3088`