Question

The formula for finding the volume of a cone is V =

1
3
πr2h. The volume of a cone is 300 cm3 and the height of the cone is 10 cm. What is the approximate radius of the cone?
A) 3 cm
B) 5 cm
C) 9 cm
D) 28 cm

Answer 1

Option B) 5 cm

Explanation:

We are given the following information in question:

Volume of cone =

`\displaystyle(1)/(3)\pi r^2h`

The volume of a cone is 300 cm cube and the height of the cone is 10 cm.

Putting the values in above equation:

`\displaystyle(1)/(3)\pi r^2h = 300\\\\r^2 = (330* 3)/(\pi * 10) = (330* 3)/(3.14 * 10) = 31.5286\\\\r = 5.615 \approx 5`

Hence, the approximate radius of the cone is 5 cm.

Answer 2

Answer: The correct option is

(B) 5.35 cm.

Step-by-step explanation: Given that the formula for the volume of a cone with radius r units and height h units is

`V=(1)/(3)\pi r^2h.`

Also, given that the volume of a cone is 300 cm³ and the height of the cone is 10 cm.

We are to find the approximate radius of the cone.

From the given formula, we can write

`V=(1)/(3)\pi r^2h\\\\\\\Rightarrow 300=(1)/(3)*(22)/(7)* r^2*10\\\\\\\Rightarrow r^2=(300*3*7)/(220)\\\\\\\Rightarrow r^2=(6300)/(220)\\\\\\\Rightarrow r^2=28.63\\\\\Rightarrow r=\pm5.35~(approx.)\\\\\Rightarrow r=\pm5`

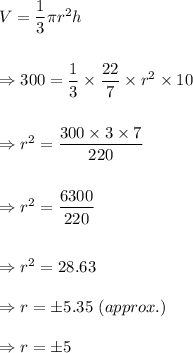
Since the radius of the cone cannot be negative, so r = 5 am.

Thus, the required approximate radius of the cone is 5 cm.

Option (B) is CORRECT.