Question

Find the sum of the first 9 terms of the following sequence. Round to the nearesthundredth if necessary.40,-16,32/5

Answer 1

The following sequence is a geometric series and we have been provided with the formula

`S_n=\frac{a_1-a^{}_1r^n}{1-r}`

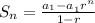
Here a1 is the first term = 40,

r is the common ratio = -0.4 (to get r, divide the second term by the first term)

n = number of terms = 9. Now let's solve

`\begin{gathered} S_n=\frac{a_1-a^{}_1r^n}{1-r} \\ \\ S_9=\frac{40_{}-40*(-0.4)^9}{1-(-0.4)} \\ \\ S_9=\frac{40_{}-(-0.0105)^{}}{1+0.4} \\ \\ S_9=\frac{40_{}+0.0105^{}}{1+0.4} \\ \\ S_9=\frac{40.0105^{}}{1.4} \\ \\ S_9=28.5789 \end{gathered}`

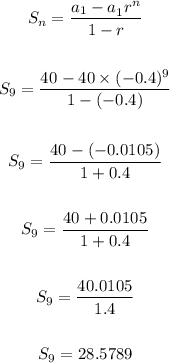
The sum to the nearest hundredth becomes = 28.58