Question

Find the a) domain, b) x-intercept and c) y - intercept: 1) f(x) = 3x-12 2x+4 2x+9 2) f(x) = x²-16 3) f(x) = x2-9

Answer 1

Check Explanation

Step-by-step explanation

Before we start answering, we should first explain what these terms stand for

- Domain

The domain of a function refers to the values of the independent variable (x), where the dependent variable [y or f(x)] or the function has a corresponding real value. The domain is simply the values of x for which the output also exists. It is the region around the x-axis that the graph of the function spans.

- x-intercept

The x-intercept refers to the value of x when the value of y or f(x) = 0, that is, the value of x at which the graph of the function crosses the x-axis. To obtain this, we just solve for x when y or f(x) = 0

- y-intercept

The y-intercept refers to the value of y or f(x) when the value of x = 0, that is, the value of y when it crosses the y-axis. To obtain this, we just substitute 0 for x and solve for f(x)

We can now solve

`f(x)=(3x-12)/(2x+4)`

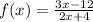
- For the domain, we can tell that x can take on any real number value and provide an answer for f(x) except the point where the denominator of this is equal to 0. At the point where the denominator is 0, f(x) will tend to infinity.

2x + 4 = 0

2x = -4

Divide both sides by 2

(2x/2) = (-4/2)

x = -2

So, the domain of this function is all real number values for x except x = -2

- For the x-intercept, we just solve for x when f(x) = 0

`\begin{gathered} f(x)=(3x-12)/(2x+4) \\ \text{when f(x) = 0} \\ 0=(3x-12)/(2x+4) \\ \text{Cross multiply} \\ 3x-12=0*(2x+4) \\ 3x-12=0 \\ 3x=12 \\ \text{Divide both sides by 3} \\ (3x)/(3)=(12)/(3) \\ x=4 \end{gathered}`

The x-intercept = 4.

In coordinate form, the x-intercept is (4, 0)

- For the y-intercept, we just solve for f(x) when x = 0

`\begin{gathered} f(x)=(3x-12)/(2x+4) \\ \text{when x = 0} \\ f(x=0)=(3(0)-12)/(2(0)+4) \\ f(x)=(0-12)/(0+4)=(-12)/(4)=-3 \end{gathered}`

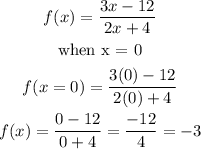
The y-intercept = -3

In coordinate form, the y-intercept is (0, -3)

For the second question

`f(x)=(2x+9)/(x-3)`

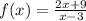
- The domain will be all real number values of x except when (x - 3) = 0

x - 3 = 0

x = 3

The domain will be all real number values of x except when x = 3.

- For the x-intercept, we just solve for x when f(x) = 0

`\begin{gathered} f(x)=(2x+9)/(x-3) \\ when\text{ f(x) = 0} \\ 0=(2x+9)/(x-3) \\ \text{Cross multiply} \\ 2x+9=0 \\ 2x=-9 \\ x=-4.5 \end{gathered}`

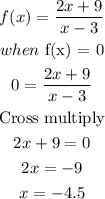
The x-intercept = -4.5

In coordinate form, the x-intercept = (-4.5, 0)

- For the y-intercept, we solve for f(x) when x = 0

`\begin{gathered} f(x)=(2x+9)/(x-3) \\ \text{when x = 0} \\ f(x=0)=(0+9)/(0-3)=(9)/(-3)=-3 \end{gathered}`

The y-intercept = -3

In coordinate form, the y-intercept is (0, -3)

For the third question

`f(x)=(x^2-16)/(x^2-9)`

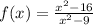
- For the domain, we first solve for when x² - 9 = 0

x² - 9 = 0

x² = 9

x = ±√9

x = ±3

x = +3 or -3

The domain of this function is all real number values of x except when x = +3 and x = -3

- For the x-intercept, we solve for x when f(x) = 0

`\begin{gathered} f(x)=(x^2-16)/(x^2-9) \\ \text{when f(x) = 0} \\ 0=(x^2-16)/(x^2-9) \\ \text{Cross multiply} \\ x^2-16=0 \\ x^2=16 \\ x=\pm\sqrt[]{16} \\ x=\pm4 \\ x=+4_{} \\ or\text{ x = -4} \end{gathered}`

The x-intercepts are at -4 and +4.

In coordinate form, the x-intercept are (-4, 0) and (4, 0)

- For the y-intercept, we solve for f(x) when x = 0

`\begin{gathered} f(x)=(x^2-16)/(x^2-9) \\ \text{when x = 0} \\ f(x)=\frac{0-16}{0^{}-9}=(-16)/(-9)=1.7778 \end{gathered}`

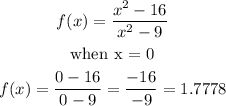
The y-intercept = (16/9) = 1.7778

In coordinate form, the y-intercept is (0, 1.7778)

Hope this Helps!!!