Question

What is the slope of a line that is perpendicular to the line whose equation is 3x+2y=6?A. −3/2B. −2/3C. 3/2D. 2/3

Answer 1

We would begin by determining the slope of the line given;

`3x+2y=6`

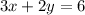
To determine the slope, we would have to express the equation of the line in slope-intercept form as follows;

`y=mx+b`

Therefore, we need to make y the subject of the equation as shown below;

`\begin{gathered} 3x+2y=6 \\ \text{Subtract 3x from both sides of the equation} \\ 2y=6-3x \\ \text{Divide both sides by 2 } \\ (2y)/(2)=(6-3x)/(2) \\ y=(6)/(2)-(3x)/(2) \\ y=3-(3)/(2)x \end{gathered}`

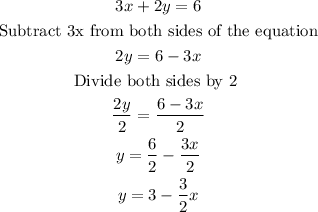
The equation in slope-intercept form appears as shown above. Note that the slope is given as the coefficient of x.

Note alo that the slope of a line perpendicular to this one would be a "negative inverse" of the one given.

If the slope of this line is

`-(3)/(2)`

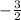
Then, the inverse would be

`-(2)/(3)`

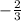
The negative of the inverse therefore is;

`\begin{gathered} (-1)*-(2)/(3) \\ =(2)/(3) \end{gathered}`

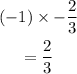
The answer therefore is option D