To begin we shall sketch a diagram of the line segments as given in the question
As depicted in the diagram, line segment AC is parallel to line segment DB.
This means angle A and angle B are alternate angles. Hence, angle B equals 41 degrees. Similarly, angle C and angle D are alternate angles, which means angle C equals 56.
Therefore, in triangle EAC,
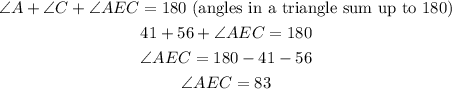
The measure of angle AEC is 83 degrees