Question

A manufacturer knows that their items have a normally distributed length, with a mean of 8.4 inches, and standard deviation of 1.4 inches.If one item is chosen at random, what is the probability that it is less than 11.8 inches long?

Answer 1

We will make use of the z-score to calculate the probability. The z-score is calculated using the formula:

`z=(x-\mu)/(\sigma)`

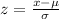
where x is the score, μ is the mean, and σ is the standard deviation.

From the question, we have the following parameters:

`\begin{gathered} x=11.8 \\ \mu=8.4 \\ \sigma=1.4 \end{gathered}`

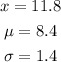
Therefore, we have the z-score to be:

`\begin{gathered} z=(11.8-8.4)/(1.4) \\ z=2.43 \end{gathered}`

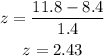
Using a calculator, we can get the probability value to be:

`P=0.9925`

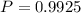
The probability is 0.9925 or 99.25%.