Question

Grade 12 math can you please explain each step, what are you doing, why and the final result that contributes to the sketch.

Answer 1

ANSWER and EXPLANATION

We want to sketch the graph of the given function:

`y=(2x^2-7x+5)/(2x-1)`

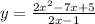
First, we have to check for the asymptotes of the function.

To find the vertical asymptote, we have to equate the denominator to 0 and solve for x:

`\begin{gathered} 2x-1=0 \\ 2x=1 \\ x=(1)/(2) \end{gathered}`

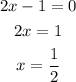
That is the vertical asymptote.

To find the horizontal asymptote, we have to check the degrees of the numerator and denominator. Since the degree of the numerator is greater than the denominator's, there is no horizontal asymptote.

To find the slant asymptote, divide the numerator by the denominator and identify the quotient:

This implies that the slant asymptote is:

`y=x-3`

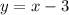
The asymptotes will provide the boundaries for the graph of the function as follows:

Now, we have to find some coordinate points that satisfy the function.

Let us solve for y for values of x = -2, -1, 0, 1, 2, 3:

`\begin{gathered} \Rightarrow x=-2 \\ y=(2(-2)^2-7(-2)+5)/(2(-2)-1)=-5.4 \\ \Rightarrow x=-1 \\ y=(2(-1)^2-7(-1)+5)/(2(-1)-1)=-4.67 \\ \Rightarrow x=0 \\ y=(2(0)^2-7(0)+5)/(2(0)-1)=-5 \\ \Rightarrow x=1 \\ y=(2(1)^2-7(1)+5)/(2(1)-1)=0 \\ \Rightarrow x=2 \\ y=(2(2)^2-7(2)+5)/(2(2)-1)=-0.33 \\ \Rightarrow x=3 \\ y=(2(3)^2-7(3)+5)/(2(3)-1)=0.4 \end{gathered}`

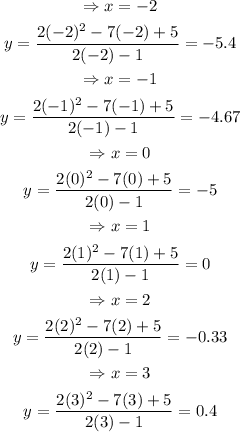
We also have to identify the x and y intercepts of the function.

For the x-intercept, solve for x when y = 0:

`\begin{gathered} 0=(2x^2-7x+5)/(2x-1) \\ \Rightarrow2x^2-7x+5=0 \\ 2x^2-2x-5x+5=0 \\ 2x(x-1)-5(x-1)=0 \\ (2x-5)(x-1)=0 \\ x=(5)/(2);x=1 \end{gathered}`

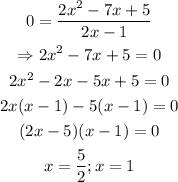
For the y-intercept, solve for y when x = 0:

`\begin{gathered} y=(2(0)^2-7(0)+5)/(2(0)-1) \\ y=(5)/(-1) \\ y=-5 \end{gathered}`

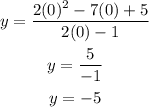
Let us draw the table of values:

Now, we can use the calculated points, the intercepts, and the asymptotes to sketch the graph of the function:

That is the sketch of the function.