Question

Please give steps and explanations to how you get the correct answer I am confused

Answer 1

To find the area under a function in a given interval you need to find the definite integral of the function in that interval.

For the given function:

`\begin{gathered} P=100(0.4)^t \\ \\ \int_0^8Pdt=\int_0^8100(0.4)^tdt \end{gathered}`

Use the next properties to find the integral:

`\begin{gathered} \int a* f(x)dx=a\int f(x)dx \\ \\ \int a^xdx=(a^x)/(\ln(a)) \end{gathered}`
`\int_0^8100(0.4)^tdt=100\int_0^80.4^tdt=100*(0.4^t)/(\ln(0.4))\lvert^8_0`

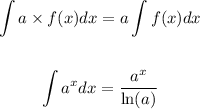
Evaluate the result for the given interval:

`\begin{gathered} (100*(0.4^8)/(\ln(0.4)))-(100*(0.4^0)/(\ln(0.4))) \\ \\ =-0.07152-(-109.13566) \\ \\ =109.06 \end{gathered}`Then, the area under the given function in the interval (0,8) is 109.06