We need to identify the true statement for every polynomial P with degree n.
The degree n of a polynomial is the exponent of the highest power of x in that polynomial. For example, the polynomial
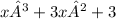
has degree 3, since the highest power of x has exponent 3.
Thus, if the degree is n, then the highest power is n (not n-1). Therefore, (a) is False.
About the number of solutions to P(x) = 0, it can equal the number of the polynomial degree. For some polynomials, the solutions can repeat, so the number of solutions will be less than n. For some of them, the solutions may not belong to the real numbers.
As an example, for P(x) = x²+4, we have:

The above polynomial has degree 2 and 2 solutions. Therefore, (b) is False.
Each turning point is where the graph of the polynomial P(x) changes from decreasing to increasing or vice versa. The graph of any polynomial of degree n has at most n-1 turning points.
Therefore, (c) is True.
We can see that (d) is False from the following example:
the line P(x) = x+1 has degree n = 1 and n = 1 x-intercept, which is its zero x = -1.
Answer:
c) The graph of P has at most n-1 turning points