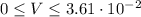Solving the equation for r:
![\begin{gathered} V=400(9.025\cdot10^(-5)-r^2) \\ r^2=9.025\cdot10^(-5)-(V)/(400) \\ r=\sqrt[]{9.025\cdot10^(-5)-(V)/(400)} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ye9yv8zgfk2w2bfgtf0q.png)
With the first equations, we can establish some limits for V:
With the lowest value for r (r=0):

With the highest value for r (r=9.5x10^-3)
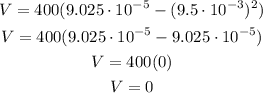
According to the radius range, velocity can be between 0 and 3.61x10^-2
It is also necessary to check the domain of the function considering it is a square root. The argument of an square root cannot be less than 0. Then:
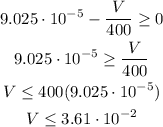
This is the same limit for velocity obtained before. Then, we can say for velocity that: