Answer:
The triangle has side lengths of 23 in, 6 in, and 28 in. is an obtuse triangle.
Explanation:
Given : A triangle has side lengths of 23 in, 6 in, and 28 in.
To Classify: It as acute, obtuse, or right.
Solution:
Let 'c' be the longest side on the set of three numbers.
If
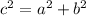 , the triangle is right
, the triangle is right
If
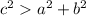 , the triangle is obtuse
, the triangle is obtuse
If
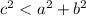 , the triangle is acute.
, the triangle is acute.
So, let a=6 , b=23 and c=28
Now we put the value in
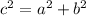 to check it is equal,greater or less.
to check it is equal,greater or less.
LHS -

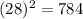
RHS -
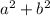
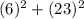
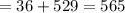
which means
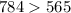
i.e, LHS > RHS
So, the triangle is an obtuse.
Therefore, The triangle has side lengths of 23 in, 6 in, and 28 in. is an obtuse triangle.