Question

I am not sure the best way to solve this problem

Answer 1

14.11 s

Step-by-step explanation

We know that in total, the runner will run a distance of 100m. He runs at constant acceleration for a while and then his velocity gets constant until the end of the track - this means that in the last part, his acceleration is zero.

So we have two parts:

For the first part, we have the acceleration and time. If we set that the initial position is zero, as shown in the diagram above, and that the runner starts from rest - therefore, his initial velocity is zero - we can find the distance of the first part of the path, which we'll call x1:

`x_1=x_0+v_0t+(1)/(2)at^2`

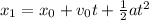
Since x0 and v0 are both zero, then those terms get cancelled:

`x_1=(1)/(2)\cdot a\cdot t^2=(1)/(2)\cdot1.5\cdot6^2=27m`

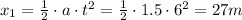
So the first part of the track, where the runner is speeding up, has a distance of 27m. Therefore, the rest of the track where the runner runs at constant acceleration is:

`100-27=73`

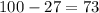
73m.

We want to find the time it took the runner to run the whole 100m. We know that he did the first part in 6 seconds. To find the time of the second part, we can use the distance we just found. Let's call it xf:

`x_f-x_1=(1)/(2)at^2+v_0t`

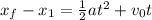
We know that the acceleration in this part of the track is zero and the initial velocity for this part is the velocity the runner had when he reached 6 seconds - i.e. 27m:

`73m=v_1\cdot t`

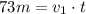
We don't know the time and we don't know the velocity, but we can find the second one using the formula for velocity for the first part of the track with t = 6s:

`\begin{gathered} v_1=a\cdot t+v_0 \\ v_1=1.5\cdot6 \\ v_1=9m/s \end{gathered}`

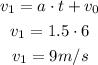
Now we can find the time for the second part of the track:

`\begin{gathered} 73m=9m/s\cdot t \\ t=(73m)/(9m/s) \\ t\approx8.11s \end{gathered}`

Therefore, the total time it took the runner to run 100m was:

`\begin{gathered} t=6s+8.11s \\ t=14.11s \end{gathered}`

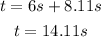
14.11 s