Question

Owners of a recreation area are adding water to a pond. The graph below shows the amount of water in the pond (in liters) versus the amount of time that water is added (in hours).Use the graph to answer the questions.(a)How much does the amount of water increase for each hour that water is added?liters=(b)What is the slope of the line?

Answer 1

GIVEN:

We are given a graph showing the increase in the amount of water pumped into a pond for every passing hour.

Required;

To determine the amount of increase in the water level for each hour that water is added.

Also, to determine the slope of the line as shown in the graph.

Step-by-step solution;

(a) Notice that the graph shows an increase in the water level for every passing hour. Notice also the following relationship;

`\begin{gathered} (hours,liter) \\ \\ (0,100) \\ \\ (1,400) \\ \\ (2,700) \\ \\ (3,1000) \end{gathered}`

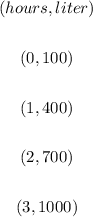
We can see that the rate of change for every hour is 300 liters increment.

Therefore, for each hour that water is added, there is an increase of 300 liters.

(b) To calculate the slope of the line shown in the graph, we shall take the change in liters and divide by the corresponding change in the hours.

We now have the following;

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \end{gathered}`

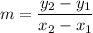
The variables are;

`\begin{gathered} (x_1,y_1)=(0,100) \\ \\ (x_2,y_2)=(1,400) \end{gathered}`

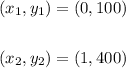
We now have the slope as follows;

`\begin{gathered} m=(400-100)/(1-0) \\ \\ m=(300)/(1)=300 \end{gathered}`

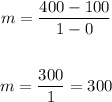
The slope therefore is 300.

ANSWER:

`\begin{gathered} (a)\text{ }Liters=300 \\ \\ (b)\text{ }slope=300 \end{gathered}`