Question

what is the smallest amount of time in which the person can accelerate the car from rest to 23 m/s and still keep the coffee cup on the roof. The coefficient of the static friction is 0.21. The maximum acceleration of the car that is allowed so that the cup does not fall is 2.1 m/s^2

Answer 1

Given:

The coefficient of the static friction, μ=0.21

The maximum acceleration of the car so that the cup does not fall, a=2.1 m/s²

The initial velocity of the car, u=0 m/s

The final velocity of the car, v=23 m/s

To find:

The smallest amount of the time in which the car can accelerate so that the coffee cup will still be on the roof.

Step-by-step explanation:

From the equation of motion,

`v=u+at`

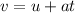
Where t is the smallest amount of time in which the person can accelerate and still keep the cup on the car.

On rearranging the above equation,

`t=(v-u)/(a)`

On substituting the known values,

`\begin{gathered} t=(23-0)/(2.1) \\ =10.95\text{ s} \end{gathered}`

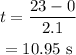
Final answer:

Thus the smallest amount of the time in which the person can accelerate the car at the given rate and still keep the cup on the roof of the car is 10.95 s