Question

What is the greatest common factor of 12xy5 + 60x4y2 − 24x3y3 ?

A. 6xy5
B. 6xy2
C. 12xy2
D. 3x4y5

Answer 1

C. 12xy2 is the awnser

Answer 2

The greatest common factor of the equation is
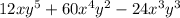`12xy^(5) + 60x^(4)y^(2)-24x^(3)y^(3)` is 12xy² .

Option (C) is correct .

Explanation:

As given the expression in the question be as follow .

`=12xy^(5) + 60x^(4)y^(2)-24x^(3)y^(3)`

Now by using the exponent formula

`x^(a)* x^(b)=x^(a+b)`

`=12xy^(2+3) + 60x^(1+3)y^(2)-24x^(2+1)y^(2+1)`

`=12xy^(2).y^(3)+ 60x^(1)x^(3)y^(2)-24x^(2)x^(1)y^(2)y^(1)`

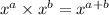
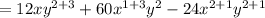
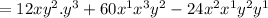
Taking common part from the above equation

`=12xy^(2)(y^(3)+5x^(3)-2x^(2)y^(1))`

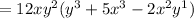
Therefore the greatest common factor of the equation is
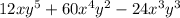`12xy^(5) + 60x^(4)y^(2)-24x^(3)y^(3)` is 12xy² .

Option (C) is correct .