Question

Evaluate the following definite integral using a geometric formula. You must show all work including the geometry area formula .

Answer 1

To evaluate the definite integral using a geometric formula, calculate the areas of the rectangles and triangles under the curve and add them together.

Step-by-step explanation:

To evaluate the definite integral using a geometric formula, you need to find the area under the curve. The formula for the area of a rectangle is A = length * width, and the formula for the area of a triangle is A = 0.5 * base * height. By dividing the interval into rectangles and triangles, you can calculate the areas and add them together to find the total area, which is the value of the definite integral.

Answer 2

Given the Definite Integral:

`\int_0^1√(1-x^2)dx`

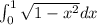
You can identify that the interval is:

`\lbrack0,1\rbrack`

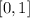
By definition, if the function is continuous and positive in a closed interval, then:

`\int_a^bf(x)dx=Area`

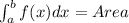
In this case, you can identify that the function is:

`y=√(1-x^2)`

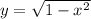
You can graph it using a graphic tool:

Since the closed interval goes from 0 to 1, you need to find this area:

You can identify that you have to find the area of a quarter circle. In order to do it, you can use this formula:

`A=(\pi r^2)/(4)`

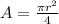
Where "r" is the radius of the circle.

In this case, you can identify that:

`r=1`

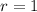
Therefore, you get:

`A=(\pi(1)^2)/(4)=(\pi)/(4)`

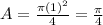
Then:

`\int_0^1√(1-x^2)dx=(\pi)/(4)`

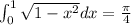
Hence, the answer is: Option D.