Question

Which of the following measurements form a right triangle? Select all that apply.

Answer 1

We are asked to find which of the measurements form a right triangle.

A right triangle is a triangle that has an angle of 90°, and also we can use the Pythagorean theorem in them.

The Pythagorean theorem tells us that the sum of the two legs of the triangle squared is equal to the hypotenuse squared:

`a^2+b^2=c^2`

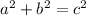
Where a and b are the legs of the triangle and c is the Hypotenuse. Also, in the right triangle, the hypotenuse is the longest side of the triangle.

We will use the Pythagorean theorem formula on all of the options using the first two given measures as a and b, and check that we the third measure as the value of c.

Option A. 7in, 24in, and 25 in.

We define:

`\begin{gathered} a=7 \\ b=24 \end{gathered}`

And apply the Pythagorean theorem:

`7^2+24^2=c^2`

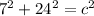
And we solve for c. If the result for x is 25, the triangle will be a right triangle, if not, this will not be an answer.

-Solving for c:

`\begin{gathered} 49+576=c^2 \\ 625=c^2 \end{gathered}`

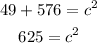
Taking the square root of both sides we find c:

`\begin{gathered} \sqrt[]{625}=c \\ 25=c \end{gathered}`

Since we get the third measure as the value of c option A is a right triangle.

Option B. 18ft, 23ft, and 29 ft.

we do the same as did with option A. First, define a and b:

`\begin{gathered} a=18 \\ b=23 \end{gathered}`

Apply the Pythagorean theorem:

`18^2+23^2=c^2`

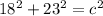
And solve for c:

`\begin{gathered} 324+529=c^2 \\ 853=c^2 \\ \sqrt[]{853}=c \\ 29.2=c \end{gathered}`

We get 29.2 instead of just 29, thus option B is NOT a right triangle.

Option C. 10in, 24in, and 26 in.

Define a and b:

`\begin{gathered} a=10 \\ b=24 \end{gathered}`

Apply the Pythagorean theorem:

`10^2+24^2=c^2`

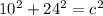
Solve for c:

`\begin{gathered} 100+576=c^2 \\ 676=c^2 \\ \sqrt[]{676}=c \\ 26=c \end{gathered}`

We get 26 which is the third measure given, thus, option C is a right triangle.

Option D. 10yd, 15yd, and 20yd.

Define a and b:

`\begin{gathered} a=10 \\ b=15 \end{gathered}`

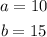
Apply the Pythagorean theorem:

`\begin{gathered} 10^2+15^2=c^2 \\ 100+225=c^2 \\ 325=c^2 \\ \sqrt[]{325}=c \\ 18.03=c \end{gathered}`

We don't get 20yd as the value of c, thus, option D is NOT a right triangle.

Option E. 15mm, 18mm, and 24 mm

Define a and b:

`\begin{gathered} a=15 \\ b=18 \end{gathered}`

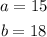
Apply the Pythagorean theorem

`\begin{gathered} 15^2+18^2=c^2 \\ 225+324=c^2 \\ 549=c^2 \\ \sqrt[]{549}=c \\ 23.43=c \end{gathered}`

We don't get 24 as the value of c, thus, option E is Not a right triangle.

Answer:

Option A and Option C are right triangles.