Your function is
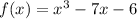
. The fundamental theorem of algebra says that there will be three roots, since the degree of the polynomial is 3. The problem provides two real roots, x = -2 and x = 3, so there must be one more.
The theorem also says that possible roots of the polynomial would be in this case, the factors of the constant (-6) over the factors of the coefficient of the term with the highest degree (1).
Factors of -6 are: 1, 2, 3, 6, -1, -2, -3, -6
Factors of 1 are: 1, -1
Possible rational roots are: 1, 2, 3, 6, -1, -2, -3, -6
I then use synthetic division to see which possible rational root is a real root by dividing
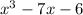
by the possible rational roots, and I get a root when the remainder is 0. Remember to put the placeholder of 0 for x^2 when dividing:
-1} 1 0 -7 -6
-1 1 6
-----------------
1 -1 -6 0
When I divide by the possible rational root of -1, I get a remainder of 0, which means -1 is a root.
To check:
(x + 2)(x - 3)(x + 1)
= (x^2 - x - 6)(x + 1)
= x^3 - x^2 - 6x + x^2 - x - 6
= x^3 - 7x - 6