Question

According to the Fundamental Theorem of Algebra, how many roots exist for the polynomial function? (9x + 7)(4x + 1)(3x + 4) = 0 1 root 3 roots 4 roots 9 roots

Answer 1

answer is b

Explanation:

Answer 2

3 roots, since the polynomial is of third degree.

This follows immediately from the zero product property: if
`ab=0`, then either
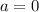
`a=0` or
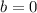
`b=0`. We have


`<span>(9x + 7)(4x + 1)(3x + 4) = 0`

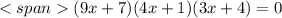
from which it follows that


`\begin{cases}9x+7=0\\4x+1=0\\3x+4=0\end{cases}`

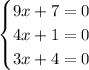
each of which admits only one solution.

Or, using the fundamental theorem of algebra, expanding we have a polynomial that is of third degree:


`</span>(9x + 7)(4x + 1)(3x + 4)=108 x^3 + 255 x^2 + 169 x + 28`

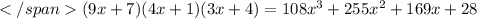
The theorem states that a polynomial
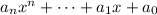
`a_nx^n+\cdots+a_1x+a_0` will have up to
`n` distinct roots. In this case, it follows that there are exactly 3, since the solutions to the system above are all distinct.