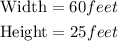If a rectangle has an area of A and sides b and h, then:
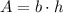
Solving for the base:

Basically, the sides b and h could have any value provided that b*h=A.
Nevertheless, this problem seems to want from us to factorize the expression:
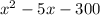
So that each side is a binomial.
Part a)
To factorize that expression, find two numbers so that if they are added up, the sum is equal to -5, and if they are multiplied, the product is equal to -300.
Since the product is negative, one number must be negative. Since the sum is negative, the biggest number should be the negative one.
Consider the factors of 300:
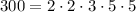
Using those factors, we can find pairs of numbers that give 300 as a result from multiplying.
After a bit of trial and error, notice that 15*20=300. If we choose 20 as the negative number, then 15*(-20)=-300 and 15+(-20)=-5. Therefore:
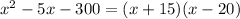
So, we can choose the width and the height to be those factors. Since (x+15) is greater then (x-20), then:
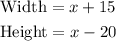
Part b)
If x=45, then: