1.
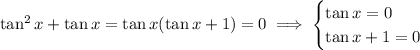
Since
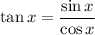
, you will have
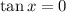
whenever
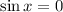
. This happens only when
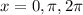
. Meanwhile,
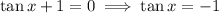
, which happens when
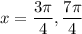
.
2.
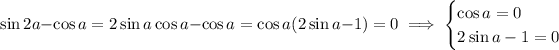
You have
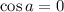
when
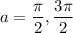
, and
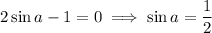
. This happens when
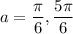
.
3.
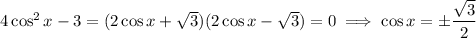
This happens when
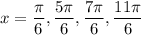
.
4.
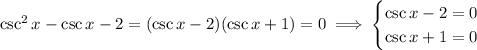
You have
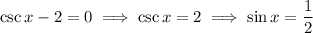
, which you know from (2) that the solutions are
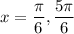
. Meanwhile,
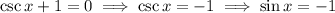
, and this happens only when
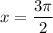
.