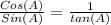Question

Tan x = sin x / cos x , therefore tan (90-A) = ? . (All angle measurements are in degrees)

Choices are below:
a. 1/tan(90-A)
b. 1/sin A
c. 1/cos(90-A)
d. 1/tan A

Answer 1

d. 1/tanA

Explanation:

In order to answer, you have to replace x=90-A in the trigonometric identity to express the tangent in function of sine and cosine.

`tan(90-A)=(sin(90-A))/(cos(90-A))`

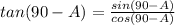
Now you have to apply the following trigonometric identities:

Sin(α-β)=Sin(α)Cos(β)-Cos(α)Sin(β)

Cos(α-β)=Cos(α)Cos(β)+Sin(α)Sin(β)

In this case, α=90 and β=A

Therefore:

`(Sin(90)Cos(A)-Cos(90)Sin(A))/(Cos(90)Cos(A)+Sin(90)Sin(A))`

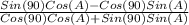
But Sin(90)=1 and Cos(90)=0

`(Cos(A))/(Sin(A)) = (1)/(tan(A))`

Answer 2

Option D.
`(1)/(tanA)`

Explanation:

tan ( 90-A ) =
`(sin(90-A))/(cos(90-A))`

since sin (90-A) = cos A

and cos (90-A) = sin A

So
`(sin(90-A))/(cos(90-A))=(CosA)/(SinA)=cot A=(1)/(tanA)`

Option D.
`(1)/(tanA)` is the correct answer.