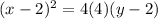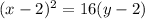Question

Using a directrix of y = −2 and a focus of (2, 6), what quadratic function is created?

Answer 1

I believe your answer is: (x-2)^2 = 16(y-2)

Answer 2

`(x-2)^2= 16(y-2)`

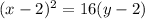
Explanation:

Using a directrix of y = −2 and a focus of (2, 6). find the quadratic function

Vertex form of a parabola is
`(x-h)^2= 4p(y-k)`

where (h,k) is the vertex and p is the distance between the vertex and focus

Vertex lies in the middle of directrix and focus

Distance between directrix and focus is 6-(-2)= 8 divide by 2 is 4

now subtract 4 from y

when parabola opens up the x value remains the same

so vertex is (2, 6-4) becomes (2,2)

Vertex is (2,2)

Distance between focus and vertex is 4 that is our p

`(x-h)^2= 4p(y-k)`

Plug in h=2 , k=2, p=4

`(x-2)^2= 4(4)(y-2)`

`(x-2)^2= 16(y-2)`