Question

Which ordered pair is a solution tothe system of inequalities shown?

Answer 1

We want to know which ordered pair is a solution of the system of inequalities shown:

`\begin{cases}x-4y\ge0 \\ x-y<-1\end{cases}`

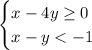
For doing so, we will try to solve both inequalities for one variable, in this case, we will use y.

On the first equation:

`\begin{gathered} x-4y\ge0 \\ x\ge4y \\ y\le(x)/(4) \end{gathered}`

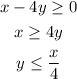
On the second equation:

For (-3, 8)

In this case, x=-3 and y=8.

`\begin{gathered} x+1=-2 \\ (x)/(4)=-(3)/(4) \\ \text{As }8>-(3)/(4),\text{ this means that (-3, 8) is NOT a solution of the system.} \end{gathered}`

For (2,5)

In this case, x=2 and y=5.

`\begin{gathered} x+1=3 \\ (x)/(4)=(2)/(4)=(1)/(2) \\ \text{As }5>(1)/(2)\text{ this means that (2, 5) is NOT a solution of the system.} \end{gathered}`

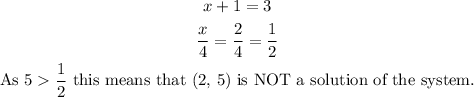
For (-7, -4)

In this case, x=-7 and y=-4.

`\begin{gathered} x+1=-6 \\ (x)/(4)=-(7)/(4) \\ \text{As }-6<-4\le-(7)/(4),\text{ (-7, -4) is a SOLUTION of the system.} \end{gathered}`

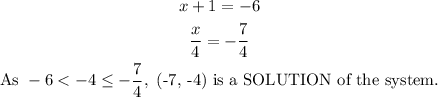
For (6, -1)

We have that x=6 and y=-1.

`\begin{gathered} x+1=7 \\ (x)/(4)=(6)/(4)=(3)/(2) \\ \text{As }7>-1,\text{ (6, -1) is NOT a solution of the system. } \end{gathered}`

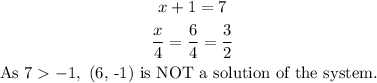
Thus, the ordered pair which is a solution of the system is (-7, -4).