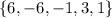A function is a relation in which each possible input value leads to exactly one output value. We say “the output is a function of the input.”
The input values make up the domain, and the output values make up the range.
The relation is given to be:
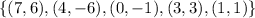
To classify a function, get the input and output values. If each input value leads to only one output value, classify the relationship as a function. If any input value leads to two or more outputs, do not classify the relationship as a function.
The input values are: {7, 4, 0, 3, 1}
The output values are: {6, -6, -1, 3, 1}
Therefore, the relation is a function.
The correct option is OPTION A: Yes, because each first component corresponds to exactly one second component.
The domain is:
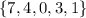
The range is: