Answer:
3√10 or about 9.49 units.
Explanation:
To find the distance between any two points, we may use the distance formula given by:
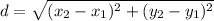
Let (3, 5) be (x₁, y₁) and (12, 2) be (x₂. y₂). By substitution:
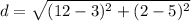
Evaluate:
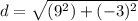
Square:
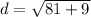
Simplify:
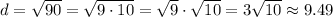
The distance between (3, 5) an (12, 2) is 3√10 or about 9.49 units.