Question

Need help figuring out if the following is Real or Complex Question number 10

Answer 1

Step-by-step explanation:

We have the expression:

`i^3`

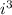
where i represents the complex number i defined as follows:

`i=√(-1)`

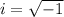
To find if i^3 is real or complex, we represent it as follows:

`i^3=i^2* i`

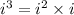
And we find the value of i^2 using the definition of i:

`i^2=(√(-1))^2`

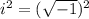
Since the square root and the power of 2 cancel each other

`\imaginaryI^2=-1`

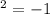
And therefore, using this value for i^2, we can now write i^3 as follows:

`\begin{gathered} \imaginaryI^3=\imaginaryI^2*\imaginaryI \\ \downarrow \\ \imaginaryI^3=(-1)*\imaginaryI \end{gathered}`

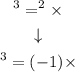
This simplifies to -i

`\imaginaryI^3=-\imaginaryI^`

Because -i is still a complex number, that means that i^3 is a complex number.

Answer: Complex