Question

Hello! I need some help with this homework question, please? The question is posted in the image below. Q15

Answer 1

A.

`x=-1,-3,11`
`f(x)=(x+3)(x-11)(x+1)`

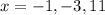
Explanation:

We have the following function:

`f(x)=x^3-7x^2-41x-33`

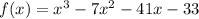
To find the zeros of the function we must set the function equal to 0 in the following way:

`x^3-7x^2-41x-33=0`

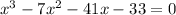
We reorganize the equation in order to be able to factor and calculate the zeros of the function, like this:

`\begin{gathered} x^3-7x^2-41x-33=0 \\ -7x^2=-8x^2+x^2 \\ -41x=-33x-8x \\ \text{ Therefore:} \\ x^3-8x^2+x^2-33x-8x-33=0 \\ x^3-8x^2-33x=-x^2+8x+33 \\ x(x^2-8x-33)=-(x^2-8x-33) \\ x^2-8x-33 \\ -8x=3x-11x \\ x^2+3x-11x-33 \\ x(x+3)-11(x+3) \\ (x+3)(x-11) \\ \text{ we replacing} \\ x(x+3)(x-11)=-1 \\ x(x+3)(x-11)+(x+3)(x-11)=0 \\ (x+3)(x-11)(x+1)=0 \\ x+3=0\rightarrow x=-3 \\ x-11=0\rightarrow x=11 \\ x+1=0\rightarrow x=-1 \end{gathered}`

Therefore, the zeros are:

`x=-1,-3,11`

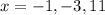
And in its factored form the expression would be:

`f(x)=(x+3)(x-11)(x+1)`