Expand the right hand side, simplify, and match up the coefficients of same-power terms.
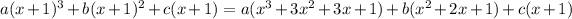
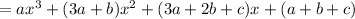
Since this must be the same as
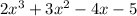
, you need to satisfy
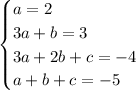
The solution for

is already given,
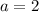
. Substitute this into the second equation to find
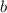
.
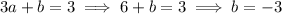
Now plug
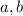
into either remaining equation to find

.
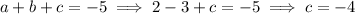
And just to check that the third equation is also satisfied,
