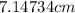Solution:
The area of a recatngle is expressed as

Given that the length of the rectangle is 13 centimeters less than four times its width, this implies that
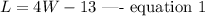
Tha area of the rectangle is 35 square centimeters. This implies that

Substitute equation 1 into equation 2. Thus,
![\begin{gathered} 36=L* W \\ \text{where} \\ L=4W-13 \\ \text{thus,} \\ 36=W(4W-13) \\ open\text{ parentheses} \\ 36=4W^2-13W \\ \Rightarrow4W^2-13W-36=0\text{ ---- equation 3} \\ \end{gathered}]()
Solve equation 3 by using the quadratic formula expressed as
![\begin{gathered} W=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}_{} \\ \text{where} \\ a=4 \\ b=-13 \\ c=-36 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/86q96e7ia1q1le9jplsi.png)
thus, we have
![\begin{gathered} W=\frac{-(-13)\pm\sqrt[]{(-13)^2-(4*4*-36)}}{2*4}_{} \\ =\frac{13\pm\sqrt[]{169+576}}{8} \\ =\frac{13\pm\sqrt[]{745}}{8} \\ =(13)/(8)\pm\frac{\sqrt[]{745}}{8} \\ =1.625\pm3.411836016 \\ \text{thus,} \\ W=5.036836016\text{ or W=}-1.786836016 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/pzr8634xxyr6t0vv7qo7.png)
but the width cannot be negative. thus, the width of the recangle is
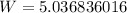
From equation 1,
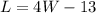
substitute the obtained value of W into equation 1.
Thus, we have
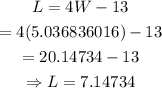
Hence:
The width is
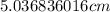
The length is